L'offre du producteur

Reprenons l'exemple de notre producteur de sabots dont la fonction de coût est C(q) = 11 q + 150 000.

Nous disions aussi que C(q)/q est le coût unitaire ou encore coût moyen. Pour une paire de sabot on avait C(1)/1 = 150 011/1 = 150 011. Pour 1 000 paires de sabots on a C(1000)/1 000 = 161 000/1 000 = 161. Pour 100 000 paires on aurait C(100 000)/100 000 = (1 100 000 + 150 000)/100 000 = 1 250 000/100 000 = 12,5. Plus le volume de production augmente plus le coût unitaire tend vers le coût marginal de 11, ici à 12,5   la paire de sabots on peut imaginer que la production serait rentable.

Mais en réalité nous avions omis un détail important, effectivement pour produire 100 000 sabots nos machines et nos locaux n'étaient pas suffisants. La fonction de coût change donc avec des coûts fixes et des coûts variables différents.

Supposons donc que pour produire jusqu'à 5 000 paires de sabots par mois, les coûts fixes soient de 150 000 €, les coûts variables sont de 11 x 5 000 = 55 000. Le coût total moyen sera de 205 000/5 000 = 41, le coût variable moyen de 55 000/5 000 = 11. Mais au-delà de 5 000 paires de sabot des coûts fixes nouveaux apparaîtront avec l'embauche d'un comptable et d'un chef d'atelier, ainsi que l'acquisition de nouveaux locaux, les coûts fixes moyens augmentent donc. Quant aux coûts variables ils vont aussi augmenter puisqu'il faudra embaucher plus de personnels donc la productivité marginale décroît. Chaque paire de sabot supplémentaire va donc coûter de plus en plus cher, ce qui montre bien la croissance du coût marginal.

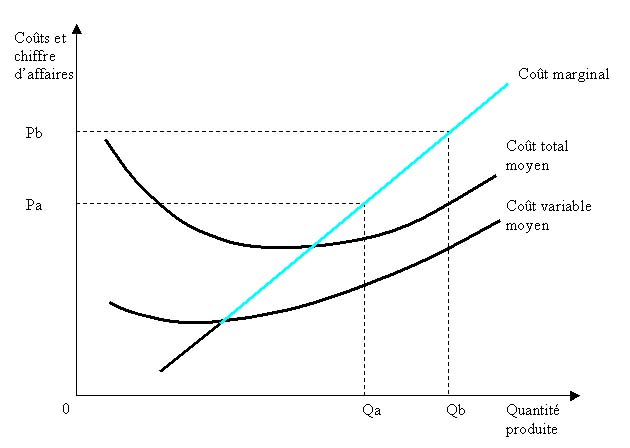
Le coût marginal est d'abord décroissant puis croissant à partir d'un certain seuil de production. La courbe d'offre individuelle correspond donc à la partie de la courbe du coût marginal, qui se situe au-dessus du point d'intersection avec la courbe de coût variable moyen. La détermination de l'offre de marché s'effectue par l'agrégation de toutes les offres individuelles. L'offre de marché met donc en relation les quantités offertes en fonction du prix. Il s'agit d'une fonction croissante en fonction du prix (élasticité positive de l'offre par rapport au prix), en effet pour un prix Pb on produit une quantité Qb, pour un prix Pa on produit une quantité Qb, sachant que si Pb > Pa alors Qb > Qa...