Le comportement du consommateur : la carte d'indifférence

On suppose que l'objectif du consommateur est d'obtenir pour sa consommation une satisfaction maximale : il voudra maximiser son utilité.

Le modèle simplifié à l'extrême donne au consommateur le choix entre un bien X et un bien Y en supposant que le consommateur préférera une combinaison des 2 biens.

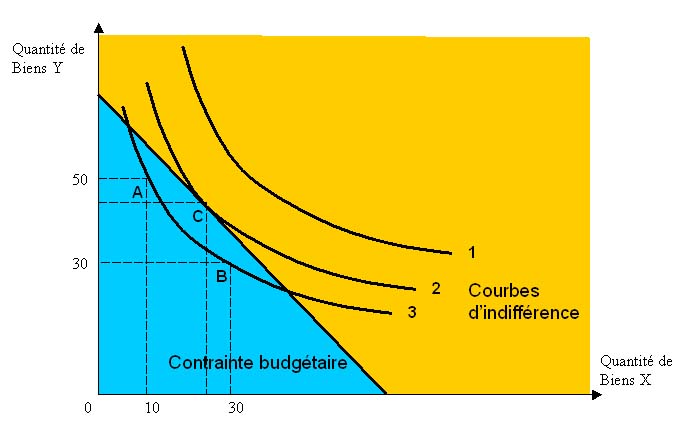
On représentera les biens X et Y dans un repère orthonormé. Chaque point représentera une combinaison des consommation de biens X et Y. Parmi ces combinaisons, certaines procureront au consommateur le même degré de satisfaction. Par exemple, ici, la combinaison A qui représente 10 unités de X et 50 unités de Y satisfait autant le consommateur considéré que la combinaison B laquelle représente 30 unités de X et 30 unités de Y.

On construira les courbes d'indifférence du consommateur en reliant entre eux les points correspondant aux paniers de consommation lui procurant le même degré de satisfaction. Ici la courbe d'indifférence n°1 reliera notamment les combinaisons A et B. L'ensemble des courbes d'indifférence sera appelé la carte d'indifférence.

Les courbes d'indifférence les plus éloignées de l'origine correspondent à des paniers de bien apportant la plus grande satisfaction au consommateur. Ici la courbe n°1 apporte une plus grande satisfaction que la courbe n°2, laquelle apporte une plus grande satisfaction que la courbe n°3.

Cependant la consommation du consommateur est limitée par ses revenus et le prix des biens. La droite de budget représente sa contrainte de revenu. Elle est de la forme R = x px + ypy, avec R représentant le revenu, x et y la quantité de biens X et Y et px, py le prix des biens X et Y.

Le consommateur ne peut se situer sur une courbe d'indifférence dont tous les points sont plus éloignés de l'origine que la droite de revenu. Il n'en a pas les moyens. Tous les paniers de biens qu'il peut atteindre sont donc situés dans la zone bleue.

Ici la satisfaction maximale est atteinte au point C puisqu'il s'agit d'un panier de biens situé sur la courbe d'indifférence la plus élevée mais qui correspond également à un point de la droite de budget.

Le consommateur n'a pas intérêt à se situer au point A, il n'y maximise pas son utilité, on suppose en effet qu'il n'épargne pas.

Exercice

Nous supposons qu'un individu quelconque, appellons le Oscar, gagne 2 000   mensuellement et qu'il consacre l'intégralité de ses revenus (eh oui, rappelons nous qu'il n'est pas censé épargner) pour se nourrir et pour se loger. X est la quantité de biens consommés pour la nourriture et Y la quantité de biens consommés pour se loger. Comme les biens X sont divers on considérera que la quantité de X correspond à la somme d'argent dépensée pour les biens X, de même on considérera que la quantité de Y est la somme d'argent consacrée au logement, que ce soit sous forme d'un montant de loyer ou de remboursement d'un prêt suite à un achat immobilier.

Ses possibilités de consommation en euros sont les suivantes :

À partir de là il est possible de représenter la droite de budget, mettez en évidence par un code couleur les paniers de biens consommables et ceux qui ne le sont pas.

Évidemment Oscar a besoin simultanément de se nourrir et de se loger, il ne pourra faire le choix de consacrer 0   à la nourriture ou 0   au logement. Oscar nous révèle ses choix de consommation à travers les choix 1 correspond à des paniers de biens qui lui sont indifférents, il nous révèle aussi ses choix 2 et ses choix 3 en nous précisons qu'il préfère le choix 1 au choix 2 et le choix 2 au choix 3. Représentez sa carte d'indifférence et son choix optimum.